I poliedri e la formula di Eulero

Si chiama poliedro la figura, la parte di spazio, delimitata dall'unione di almeno 4 poligoni, ciascuno appartenente ad un piano differente e nel quale ogni lato sia l'intersezione di due di questi poligoni.

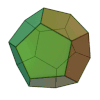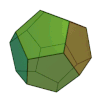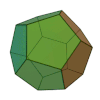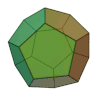
I poliedri sono regolari se le facce sono poligoni tutti uguali, essi sono anche detti solidi platonici per la valenza simbolica ad essi assegnata dal filosofo greco Platone, i poliedri regolari sono: il tetraedro, il cubo (esaedro), l'ottaedro, il dodecaedro e l'icosaedro.

POLIEDRI REGOLARI 

 modelli 3D tratti da https://it.wikipedia.org/wiki/Solido_platonico

A volte conviene sviluppare i solidi in un piano, cioè riportarli su di uno stesso piano immaginando di 'aprirli' e di distenderne le facce, ciò facilita ad esempio il calcolo del perimetro e dell'area dell'intera superficie della figura.

Lo studio dei poliedri occupa un posto centrale nella geometria greca, si deve però a Cartesio e ad Eulero la scoperta di una curiosa proprietà che lega il numero dei vertici, il numero dei lati ed il numero delle facce di un poliedro semplice (cioè di un un poliedro senza “buchi”), che sia regolare o meno.

Dato un poliedro semplice, se chiamiamo V il numero dei suoi vertici, E il numero dei suoi lati (o spigoli), F il numero delle sue facce, allora si può dimostrare che:

V – E + F = 2

Così, nel semplice esempio di un cubo:

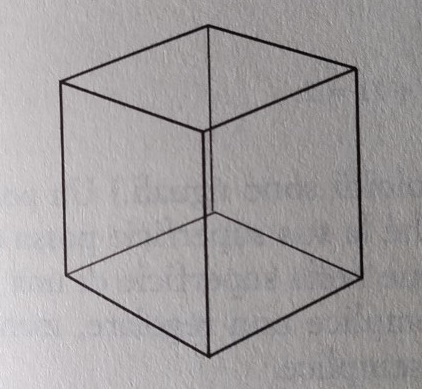
V – E + F = 8 – 12 + 6 = 2

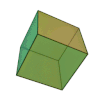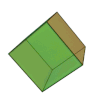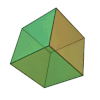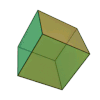
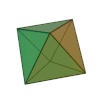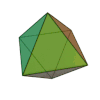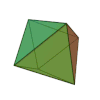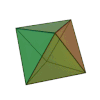
ma non è richiesto che il poliedro sia regolare, come in questo esempio:

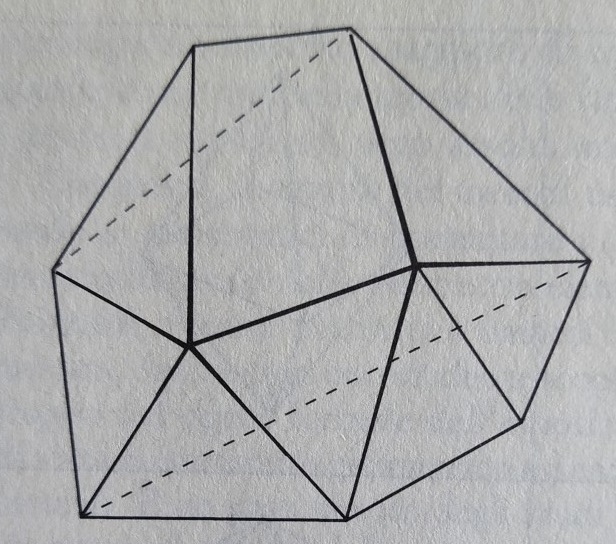
V – E + F = 9 – 18 + 11 = 2

Servendosi di questa formula si può anche dimostrare algebricamente che i poligoni regolari non possono essere più di cinque.

Il campo di validità di questa proprietà si estende ben oltre i poliedri della geometria elementare, con le facce piane e gli spigoli rettilinei; la formula riguarda solo il numero di vertici, spigoli e facce, si può applicare bene anche a poliedri con facce e spigoli curvilinei.

* "Che cos'è la matematica?" – R. Courant, H. Robbins – Universale Bollati Boringhieri