Il navigatore satellitare, la Ricerca Operativa e l'algoritmo di Dijkstra

 

Qualche tempo fa prima di cominciare un viaggio in automobile, per andare in vacanza o per lavoro o per raggiungere qualche familiare lontano, si chiedeva consiglio o si studiava il tragitto a tavolino, su di una carta stradale.

Anche se avere una cartina stradale in macchina può ancora tornare utile, da qualche anno le abitudini sono cambiate: ci si siede in macchina, si imposta la destinazione sul navigatore satellitare e si parte! Il navigatore ci fornisce un'ottima approssimazione della distanza totale da percorrere, del tempo che impiegheremo e ci guida passo passo avvisandoci delle svolte, degli incroci, dei semafori... e se non seguiamo le sue indicazioni ricalcola il percorso e pazientemente ricomincia. Ma come è possibile?

Il navigatore satellitare dispone di un'antenna e utilizza il sistema GPS (Global Positioning System) per la geo-localizzazione cioè per l'individuazione della posizione del dispositivo sulla superficie terrestre, in termini di latitudine e longitudine, nonché per conoscere con precisione l'ora esatta. Grazie ad una rete di una trentina di satelliti artificiali in orbita, rete di derivazione militare, la ricezione di segnali radio da almeno 4 satelliti permette al terminale di elaborare la propria posizione, con un margine di errore al momento di pochi metri.

Il navigatore satellitare deve poter accedere ad una cartografia, e disporre quindi di una memoria esterna, di un database con informazioni sulle mappe geografiche (nomi e lunghezze delle vie urbane ed extraurbane, informazioni sul senso di percorrenza di un tratto stradale, sull'accessibilità dello stesso, limiti di velocità, ecc.) ma vi si possono aggiungere anche altre informazioni come la presenza di ospedali e farmacie, di distributori di benzina, di luoghi turistici interessanti. La disponibilità di mappe ed informazioni aggiornate, spesso a pagamento, è evidentemente condizione necessaria per il buon funzionamento del sistema.

Il cuore di un sistema di navigazione, ancora una volta sta però nel software, in un algoritmo di path finding, un algoritmo per l'individuazione del cammino di lunghezza minima dalla posizione attuale ad una particolare destinazione. I vari produttori di navigatori satellitari (e in modo analogo vale anche per servizi web come ad esempio www.viamichelin.it) utilizzano algoritmi proprietari, ciascuno con l'aggiunta di qualche euristica ad algoritmi generali, nel tentativo di migliorare le performance rispetto alla concorrenza.

 

Voglio qui soffermarmi su un algoritmo per l'individuazione del cammino minimo, l'Algoritmo di Dijkstra, capostipite e ossatura di vari programmi di path finding. Esso fa parte di quel mare magnum di problemi e algoritmi affrontati dalla Ricerca Operativa, una branca della matematica applicata, una disciplina nata nel corso della II guerra mondiale per occuparsi di problemi di decisione, applicando un approccio scientifico a problemi di ottimizzazione di sistemi organizzativi complessi. Ovviamente, un importante fattore del suo successo nella soluzione di problemi è derivato dallo sviluppo di potenti calcolatori elettronici, faccio notare che tale relazione si può però anche invertire, la ricerca operativa ha sicuramente contribuito in modo importante alla nascita ed allo sviluppo dei computer. La ricerca operativa ha individuato nel tempo categorie comuni di problemi (assegnazioni, scheduling, code...) ed oggi supporta il settore pubblico e quello privato con applicazioni che vanno dall'urbano sociale (gestione dei rifiuti, orari dei mezzi pubblici, gestione del traffico, dell'assistenza familiare, degli affollamenti, ...), alla salute (pianificazioni, diagnostiche, costruzioni di indici, ...), ad applicazioni militari (logistiche di distribuzione e approvvigionamenti, gestione dei salvataggi, …), ai servizi (assicurazioni e rischi, strategie di assunzioni, pubblicità, ...), alle industrie (gestione dei programmi di produzione, distribuzione dei prodotti, test di sicurezza, controllo qualità, ...).

 

Una sezione della letteratura della ricerca operativa riguarda i problemi di percorso ottimo nei quali vi è una funzione oggetto da minimizzare o massimizzare ed un sistema di vincoli da rispettare, si tratta di problemi che vengono affrontati tipicamente con l'uso della teoria dei grafi (per un'introduzione ai grafi si veda in questo stesso sito la storia “Eulero ed i ponti di Kőnigsberg”). In relazione alla tipologia dei vincoli si identificano 3 differenti classi di sotto-problemi: a) il cammino non deve rispettare alcun obbligo di passaggio b) il cammino deve visitare obbligatoriamente uno o più nodi della rete, eventualmente tutti (problemi hamiltoniani) c) il cammino deve attraversare obbligatoriamente alcuni archi della rete (problemi euleriani). I problemi di percorso ottimo si complicano a piacere se si utilizzano più veicoli, se i veicoli hanno differenti capacità di servizio, se si hanno molteplici punti di partenza, se i dati non sono deterministici bensì aleatori, se si introducono vincoli di tipo temporale.

 

Dal punto di vista computazionale i problemi della prima categoria, ovvero i problemi di individuazione di un percorso ottimo tra due nodi della rete senza particolari obblighi di passaggio, sono i più semplici da trattare, a questi appartiene l'algoritmo ideato alla fine degli anni '50 dal matematico olandese E. W. Dijkstra. Vediamolo in azione con un esempio: si abbia un grafo orientato con lunghezze degli archi l tutte positive (esse rappresentano i 'costi', potrebbero ad esempio indicare i chilometri o i tempi necessari per transitare da un nodo ad un altro), vogliamo determinare il percorso minimo tra i nodi r (la sorgente) ed s (la destinazione) della rete. Ogni nodo v riceve un'etichetta d_v che può variare nel corso dello svolgimento dell'algoritmo e che rappresenta la lunghezza del cammino più breve sinora individuato da r a v. Nelle rappresentazioni dei grafi verranno segnate in nero le etichette provvisorie, in rosso quelle definitive.

 

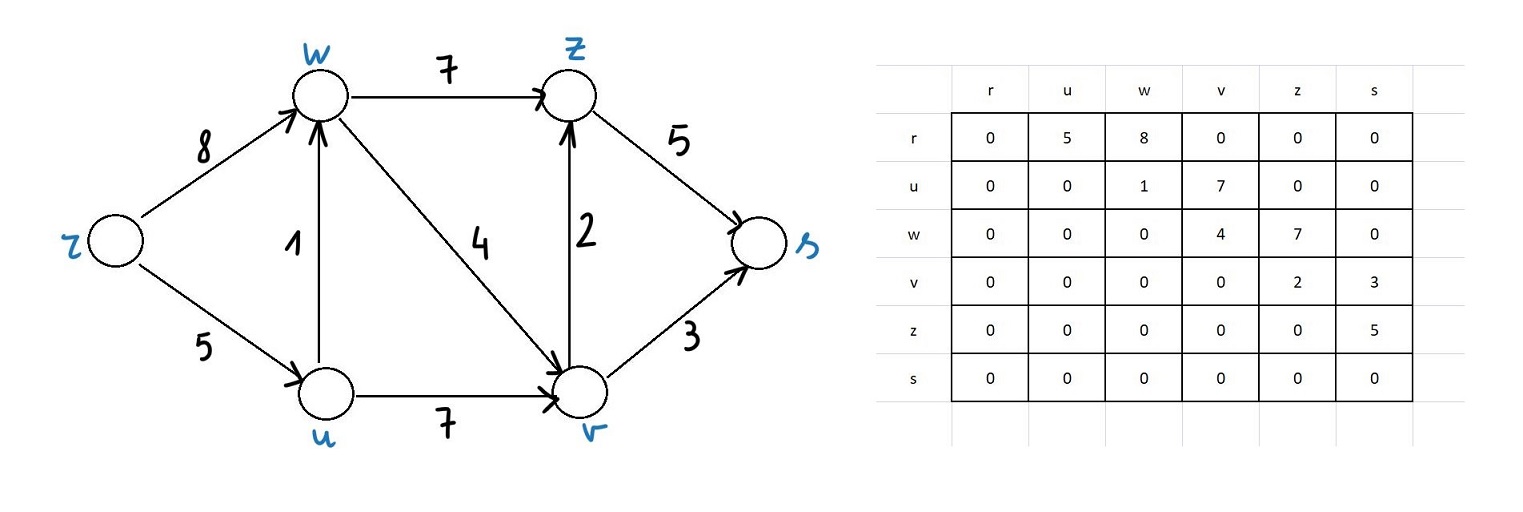
Un grafo e la corrispondente matrice dei costi, uno dei modi per trattare in modo informatico i dati del problema

 

Passo 1) Poniamo d_r = 0 e d_u = +∞ per tutti gli altri nodi u. L'etichetta di d_r è definitiva, tutte le altre sono provvisorie.

Passo 2) Sia u l'ultimo vertice la cui etichetta è stata dichiarata definitiva. Si considerino tutti gli archi del tipo (u, v) uscenti da u e si aggiorni l'etichetta di ogni vertice v, successore di u come segue: se d_v > d_u + l(u, v) allora d_v = d_u + l(u, v)

Passo 3) Scegliere il vertice w che ha etichetta minima tra tutte quelle provvisorie e dichiararla definitiva. Se esistono archi uscenti da w allora si torni al passo 2), in caso contrario Stop, l'algoritmo è terminato.

 

 

  

 

 

 

 

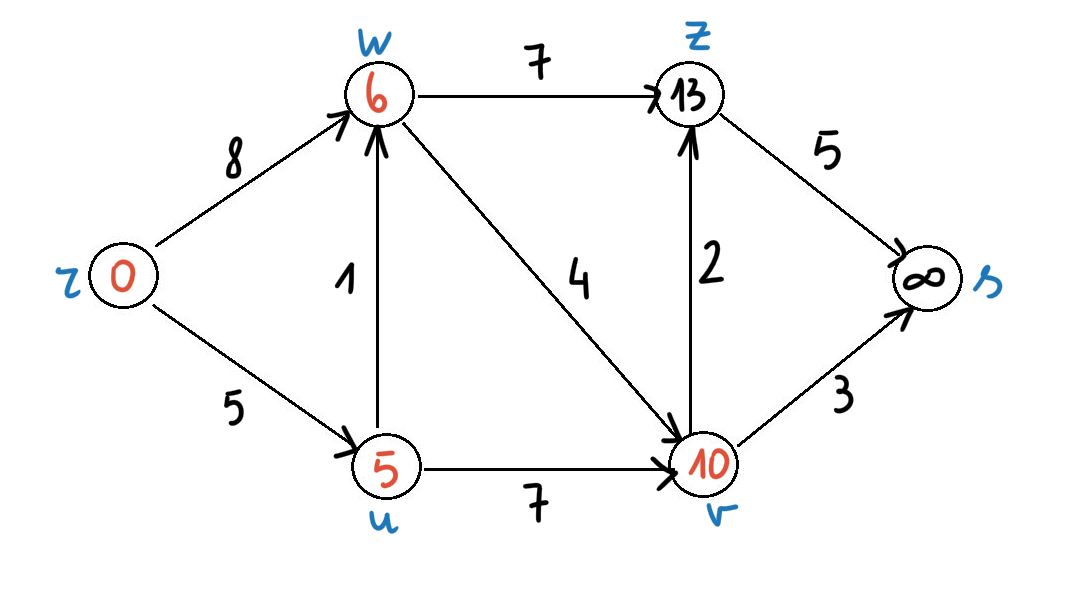
L'algoritmo si espande 'a macchia d'olio' e ad ogni iterazione, dopo l'aggiornamento, l'etichetta del nodo corrente v indica la lunghezza di un percorso da r a v che contiene come nodi intermedi solo vertici dichiarati definitivi, ciò è garanzia di ottimalità per il risultato finale.

 

 

 luglio 2020

* - Lezioni di Ricerca Operativa – F. Mason – Cafoscarina ed.

- Algoritmi – T. Cormen, C. Leiserson, R. Rivest – Jackson libri

- Statistica vol. 3 – Statistica industriale e ricerca operativa - A. Boggio, G. Borello – Petrini