QUADRATI MAGICI
E’ possibile sistemare le 9 cifre in una griglia quadrata 3x 3 in modo che la somma dei numeri di ogni riga, colonna e diagonale sia la stessa?
Questo è forse il più antico esempio di “matematica ricreativa”, anche se con simboli differenti, da quattro millenni in Cina si attribuiscono a questo quadrato, il quadrato di Lo Shu, proprietà mistiche, esso è stato riprodotto in tanti talismani ed amuleti portafortuna.
Narra una delle leggende in proposito che, a seguito di una devastante inondazione del fiume Lo, la popolazione offrì sacrifici al dio del fiume per placarne l’ira, ogni volta però appariva una tartaruga che passava senza interesse vicino al sacrificio e l’inondazione continuava a perdurare. La tartaruga venne interpretata come un messaggero del dio del fiume, un dio che però continuava a rifiutare i sacrifici, quante volte dovevano essere ripetuti i sacrifici perché il dio fosse soddisfatto? Finalmente un bambino notò che la tartaruga aveva sul dorso segni che formavano un quadrato (una particolare disposizione con i numeri pari collocati proprio negli angoli del quadrato), la somma per riga, per colonna ed in diagonale dava lo stesso numero, il numero 15, questo era il messaggio, questa era la risposta che aspettavano e presto la piena del fiume terminò!
Un quadrato magico allora è una matrice, una griglia quadrata (3 per 3 o più) dove in ogni cella vengono collocati numeri interi. Il numero di righe e di colonne è detto ordine e la somma per linea è detta costante del quadrato magico o totale magico, se n è l’ordine del quadrato il numero degli elementi presenti nel quadrato è sempre n2. Aggiungendo una stessa quantità ad ogni numero oppure moltiplicando tutti i numeri per una stessa quantità, si ottiene ovviamente ancora un quadrato magico. La somma dei primi 9 numeri dà 45, così dividendo 45 per 3 (il numero di righe/colonne) il risultato 15 non è altro che la somma per ogni linea, questa è la costante del quadrato di Lo Shu.
Dato un quadrato magico con delle rotazioni si può ottenere un altro quadrato magico e all’aumentare del numero dell’ordine cresce anche il numero di quadrati magici: con ordine 4 se ne creano 880 a somma 34, esistono centinaia di milioni di quadrati magici di ordine 5 mentre il numero di quadrati magici di ordine 6 non è stato ancora calcolato.
Lungo la Via della Seta oltre alle mercanzie circolarono anche le idee cinesi, l’idea dei quadrati magici si diffuse anche ad altre culture e nazioni, l’India, il mondo arabo e finalmente l’Europa e da qui nel Nuovo Mondo, l’America.
Molti matematici ma anche artisti e persone comuni subirono il fascino di queste sequenze, sono stati ‘scoperti’ quadrati magici di varie dimensioni 4x4, 5x5, … quadrati con numeri primi, con i numeri di Fibonacci, cubi magici… fino al più grande QM esistente con tutti i primi n2 numeri naturali, il “quadrato magico dei vampiri” di A. Graziotti, Guinness dei primati del 1989, un quadrato di ordine 64, con i primi 4096 numeri naturali, nessuno escluso, la cui costante è 131.104.
Un quadrato magico di ordine 4 appare nella famosa incisione di Albrecht Dürer, Melancholia, del 1514, l’opera ritrae una figura alata pensosa e circondata da simboli appartenenti al mondo dell’alchimia, tra questi, in alto a destra, un quadrato magico che riporta anche la data dell’incisione.

Immagine: Wikipedia
Anche Benjamin Franklin scoprì un quadrato magico, ne andava molto fiero e ne parlava così: “il quadrato magico più magicamente magico mai creato da un mago”. Si tratta di un quadrato magico di ordine 8, di costante 260, in realtà imperfetto nel senso che la costante non vale per le diagonali ma che presenta varie belle particolarità, ad esempio ciascuno dei 4 quadrati 4x4 è a sua volta un quadrato magico di costante 130 e 130 è anche la somma dei numeri ai quattro angoli e dei quattro numeri centrali.

Il quadrato magico di Benjamin Franklin
Un quadrato magico è all’ingresso della basilica della Sagrada Familia (Barcellona), è di ordine 4 e la costante è 33, l’età di Gesù Cristo quando venne crocifisso.

Quadrato magico all’ingresso della basilica della Sagrada Familia (Barcellona)
C’è un modo per calcolare matematicamente la costante di un quadrato magico dato il suo ordine n? La risposta è sì, e dipende dal fatto che un quadrato magico si ottiene da una serie di numeri naturali consecutivi, opportunamente permutati.
I numeri
1, 2, 3, 4, … , n
formano tecnicamente una progressione aritmetica, cioè una successione nella quale la differenza tra un termine (a partire dal secondo) ed il precedente si mantiene costante; tale costante si chiama ragione della progressione aritmetica e qui vale 1. In una progressione aritmetica dati il primo numero e la ragione è facile calcolare l’ennesimo valore della sequenza, è facile anche calcolare la somma dei termini di una progressione aritmetica con l’uso della formula seguente:
Sn = n (a1 + an) / 2
dove a1 è il primo termine e an è l’ennesimo termine della progressione.
Se abbiamo un quadrato magico di ordine n il primo termine della sequenza di elementi utilizzata è 1 e l’ennesimo termine è n2, allora applicando la formula precedente risulta che la somma dei termini è:
Sn = n2 (1 + n2) / 2
e dividendo per n, l’ordine della matrice, cioè il numero di righe o colonne... arriviamo al totale per linea cioè la costante del quadrato magico:
costante “magica” = n (1 + n2) / 2
Proviamo a vedere se la formula trovata funziona con il Lo Shu: essendo un quadrato magico di ordine 3 risulta c = 3 (1 + 9) / 2 = 15, voilà! In un quadrato magico di ordine 4 risulterebbe c = 4 (1 + 16) / 2 = 34 e così via.
Dopo aver affrontato la formula per calcolare la costante magica chiudiamo questo articolo descrivendo un algoritmo per costruire un quadrato magico di ordine 4 costruendo il quale potremo stupire i nostri amici. L’algoritmo è il seguente:
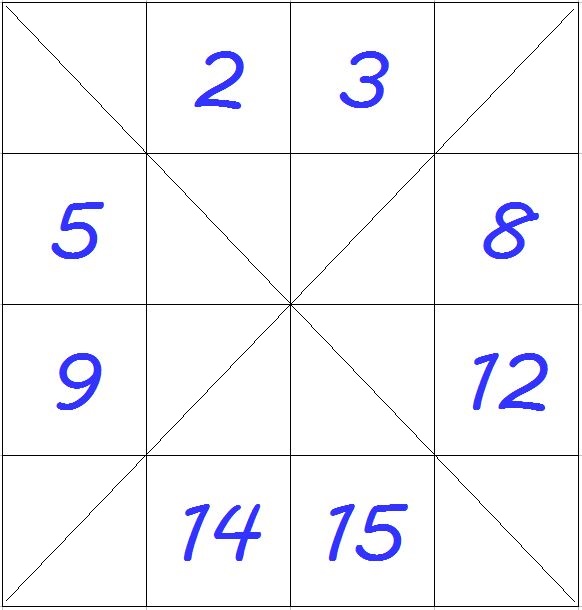
Passo 1) In una griglia 4x4 disegniamo le 2 diagonali, in modo da ‘coprire’ molte celle

Passo 2) Disponiamo i numeri come se fossero in successione, occupando però solo le celle ‘libere’ dalle linee di intersezione (1 no, 2 sì, 3 sì, 4, no, ...)
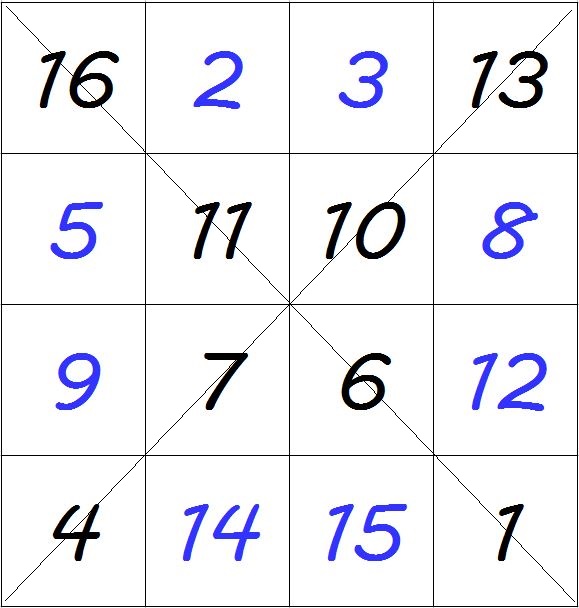
Passo3) Iniziando dall’angolo in basso a destra e ci spostiamo in orizzontale verso sinistra e poi alla riga superiore inserendo nelle celle ‘coperte’ i numeri non ancora sistemati (1, 4, 6, ...)
Ultimissima curiosità: ecco il logo dei Ragionieri Commercialisti Italiani, vi ricorda niente?

- Labirinti, quadrati magici e paradossi logici – Marcel Danesi – Ed. Dedalo
- Il libro della Matematica – autori vari - Ed. Gribaudo
- Mateureka, il Museo del Calcolo e della Matematica – Pennabilli (RN)